반응형
시그모이드(Sigmoid) 함수의 수식은 아래와 같습니다.
$y = \frac {1}{1+e^{-x}}$
시그모이드 계층의 순전파는 위의 식을 그대로 구현하면 되고, 역전파를 위해 시그모이드 함수의 미분을 정리해보겠습니다.
$\frac{\partial{y}}{\partial{x}} = \frac{\partial(1+e^{-x})^{-1}}{\partial{x}} \\ ~~~~~ = (-1) \frac{1}{(1+e^{-x})^2}(1+e^{-x})' \\ ~~~~~ = \frac{e^{-x}}{(1+e^{-x})^2} = \frac{1 + e^{-x} - 1}{(1+e^{-x})^2} \\ ~~~~~ = \frac{1+e^{-x}}{(1+e^{-x})^2} + \frac{-1}{(1+e^{-x})^2} \\ ~~~~~ = \frac{1}{1+e^{-x}} - \frac{1}{(1+e^{-x})^2} \\ ~~~~~ = \frac{1}{1+e^{-x}}(1-\frac{1}{1+e^{-x}}) \\ ~~~~~ = y(1-y)$
따라서 우리는 시그모이드 계층의 역전파를 아래와 같이 나타낼 수 있습니다.
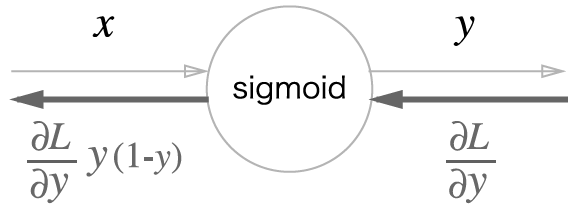
Sigmoid 계층을 클래스로 구현해보겠습니다.
class Sigmoid(object):
def __init__(self):
self.out = None # 인스턴스 변수 Out (위 식에서 y에 해당)
def forward(self, x):
out = 1 / (1 + np.exp(-x)) # 그냥 순전파
self.out = out # 역전파때 사용할 y
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out # y를 그대로 다시 사용
return dx순전파의 출력을 역전파 때 다시 사용해야하므로 인스턴스 변수에 저장해놓고 사용합니다.
읽어주셔서 감사합니다 ^^
반응형
'머신러닝, 딥러닝 ML, DL > 이론' 카테고리의 다른 글
| [Deep Learning] 9. CNN, 합성곱 계층, 패딩, 스트라이드 (2) | 2021.08.11 |
|---|---|
| [Deep Learning] 8. 합성곱 신경망, CNN의 구조 (0) | 2021.08.11 |
| [Deep Learning] 6. 경사 하강법, 기울기 (2) | 2021.08.04 |
| [Deep Learning] 5. 배치, 미니배치, 수치 미분, 기울기 (0) | 2021.08.04 |
| [Deep Learning] 4.신경망 학습, 손실 함수(오차제곱합, 교차 엔트로피 오차) (2) | 2021.07.28 |